![]()
Filters help to clear noise from signals. They are often used to clean up Analog Inputs. To accomplish this, they take the input signal value and average it with past values.
 Let’s look at the filter equation on the right:
Let’s look at the filter equation on the right:
- Input is the incoming signal value
- Output is the result of the filter
- Weight is how much influence you want past values to hold. Higher numbers place more importance on past values. Weight must be greater than 1.
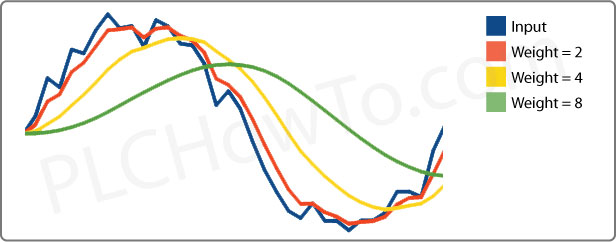
In this example we see that as Weight increases 3 things happen:
- The signal smooths out
- The Maximum and Minimum values decrease.
- Changes in input take longer to detect.
With Filters, its a balancing act, where these considerations must be balanced to arrive at an ideal Weight for your situation.
One option that isn’t in the equation but matters a great deal: The frequency samples are taken. This will effect how fast the Filter responds to changes in amplitude. In this example we took 36 samples for the single wave.
For those of you who would like to see some numbers, here they are for the example above:
| Input | Weight = 2 | Weight = 4 | Weight = 8 |
|---|---|---|---|
| 141 | 141 | 141 | 141 |
| 159 | 150 | 143.25 | 141.28 |
| 196 | 173 | 150.69 | 142.46 |
| 187 | 180 | 158.02 | 144.4 |
| 225 | 202.5 | 169.14 | 147.49 |
| 221 | 211.75 | 179.79 | 151.53 |
| 244 | 227.88 | 191.81 | 156.57 |
| 260 | 243.94 | 204.84 | 162.6 |
| 246 | 244.97 | 214.87 | 169.13 |
| 248 | 246.48 | 222.78 | 175.84 |
| 227 | 236.74 | 226.27 | 182.14 |
| 254 | 245.37 | 231.04 | 188.26 |
| 248 | 246.69 | 234.95 | 194.09 |
| 231 | 238.84 | 235.93 | 199.32 |
| 229 | 233.92 | 235.43 | 203.84 |
| 211 | 222.46 | 232.18 | 207.38 |
| 169 | 195.73 | 223.07 | 209.34 |
| 183 | 189.37 | 214.64 | 210 |
| 165 | 177.18 | 205.28 | 209.41 |
| 133 | 155.09 | 192.73 | 207.33 |
| 105 | 130.05 | 177.06 | 203.54 |
| 83 | 106.52 | 159.43 | 198.03 |
| 64 | 85.26 | 140.88 | 190.89 |
| 56 | 70.63 | 123.32 | 182.44 |
| 71 | 70.82 | 110.19 | 173.41 |
| 54 | 62.41 | 98.25 | 164.01 |
| 54 | 58.2 | 88.24 | 154.54 |
| 44 | 51.1 | 78.95 | 145.09 |
| 54 | 52.55 | 72.35 | 136 |
| 54 | 53.28 | 67.58 | 127.45 |
| 62 | 57.64 | 65.1 | 119.65 |
| 83 | 70.32 | 66.4 | 113 |
| 83 | 76.66 | 68.97 | 107.49 |
| 78 | 77.33 | 71.06 | 102.94 |
| 124 | 100.66 | 78.46 | 99.88 |
| 150 | 125.33 | 90.18 | 98.67 |


Leave a Reply